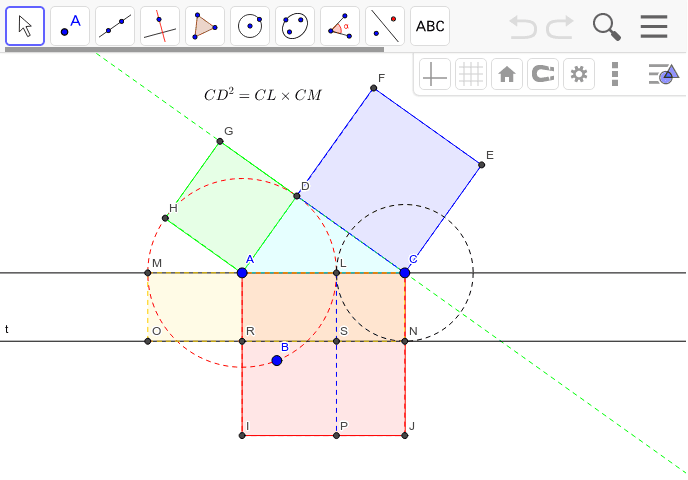
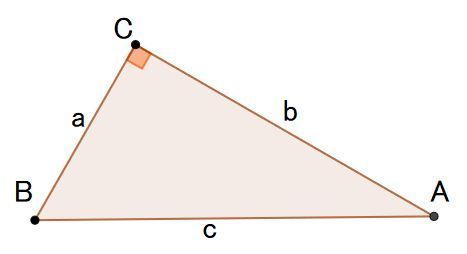
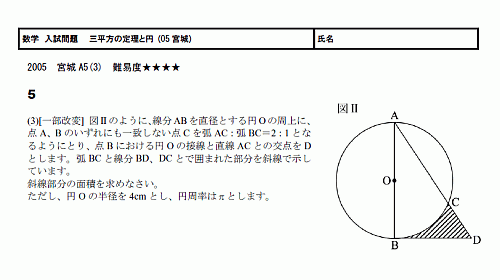
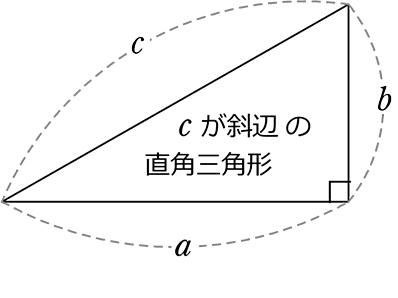
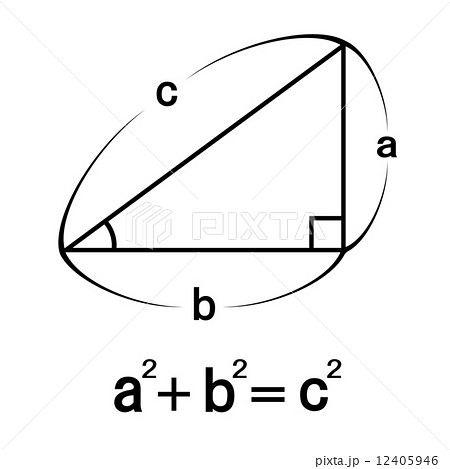
三平方の定理の証明5選直角三角形や正方形を重ねましょう 三平方の定理(別名ピタゴラスの定理)とは、底辺が $a$、高さが $b$、斜辺が $c$ である直角三角形において、$$a^2b^2=c^2$$ が成り立つことでしたね。
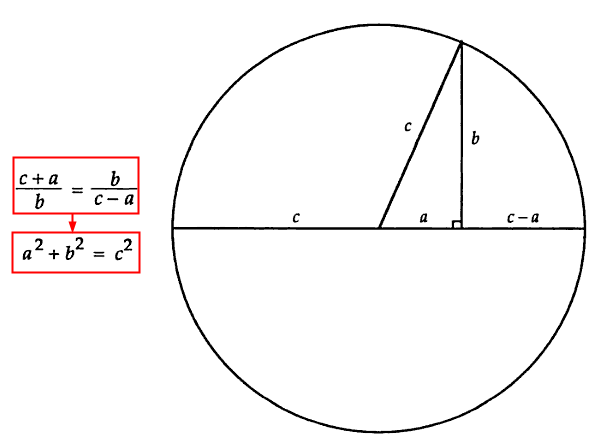
三 平方 の 定理 円-三平方の定理を少し変形すると c 2 = a 2 b 2 → c = √a2 b2 √ a 2 b 2 a 2 = c 2 b 2 → a = √c2 − b2 √ c 2 − b 2 b 2 = c 2 a 2 → b = √c2 − a2 √ c 2 − a 2 すなわち ・ 斜辺 = √( 他 の 辺)2 ( 他の活用, 平方根の計算などを基礎的・基本的な内容して活用していく.また,発表する機会を授業 内で多く設け,全体で問題解決をしていこうと考える. 1 三平方の定理に関心を持ち,直角三角形の性質を調べようとしたり,定理を活用 しようとする.
三 平方 の 定理 円のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
 |  |  |
「三 平方 の 定理 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「三 平方 の 定理 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三 平方 の 定理 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  |  |
「三 平方 の 定理 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 | ||
「三 平方 の 定理 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「三 平方 の 定理 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「三 平方 の 定理 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「三 平方 の 定理 円」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |
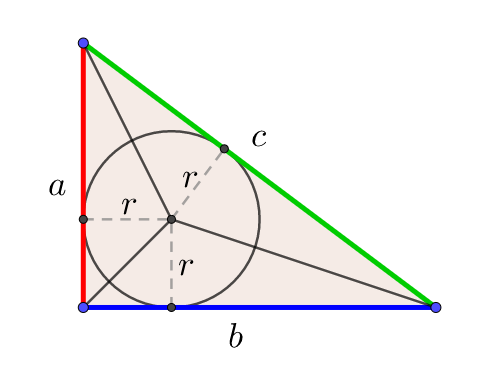
が成り立ちます。これで、三平方の定理を証明することができました!「平方」とは 2乗のことなので、「三平方の定理」と言われるゆえんは、直角三角形の「三」つの辺それぞれの「平方」、つまり a 2, b 2, c 2 の間に成り立つ関係式ということですね。 ヘロンの公式の図解 Step① 内接円の性質から S = s r Step② s − a, s − b, s − c を見つける Step③ A P ′ = s を示す Step④ A P O と A P ′ O の相似 Step⑤ C O P と O ′ C P ′ の相似 Step⑥ (1), (2), (3) を解く 三角関数を用いた証明





0 件のコメント:
コメントを投稿